This hanging mathematical problem is taking the internet by storm. Can you solve Amazon’s hanging cable interview question?

This hanging mathematical problem shared by an anonymous reader is taking the internet by storm. Also known as the catenary curve, this hanging mathematical problem was allegedly asked during an Amazon Interview. However, the problem is much older and first discovered by Robert Hooke in the 1670s, and its equation was derived by Leibniz, Huygens, and Johann Bernoulli in 1691.
The catenary curve has a U-like shape, superficially similar in appearance to a parabolic arch, but it is not a parabola. It is a curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends. Catenaries and related curves also have many other applications including architecture and engineering (e.g., in the design of bridges and arches so that forces do not result in bending moments).
For example, in the offshore oil and gas industry, “catenary” refers to a steel catenary riser, a pipeline suspended between a production platform and the seabed that adopts an approximate catenary shape. In the rail industry, it refers to the overhead wiring that transfers power to trains.
Below is the question. See if you can solve the question.
“A cable of 80 meters is hanging from the top of two poles that are both 50 meters off the ground. What is the distance between the two poles (to one decimal point) if the center cable is (a) 20 meters off the ground and (b) 10 meters off the ground?”
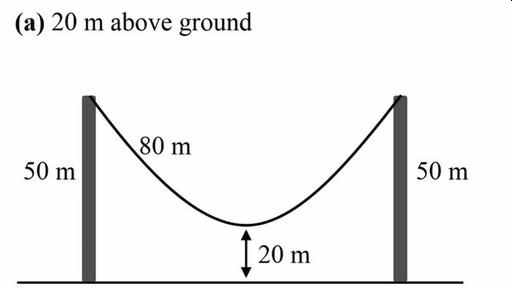
(b) 10 m above the ground
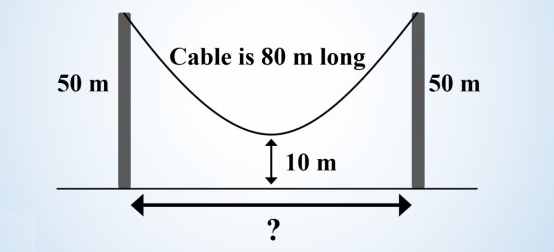
Hint: The solution to the first question (a) is described in Chatterjee and Nita (2010) and requires some knowledge of math or physics. For (b), you have to think beyond the mathematical formulas. Question (b) looks complex but a lot easier to solve with no need to use any mathematical formula. You just need simple logic with a little bit of thinking.
Below is a video of how to solve the two problems.




