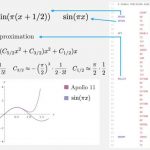
1969 Apollo 11 used these 30 lines of assembly language code to calculate transcendental functions for navigation
The successful launch of SpaceX Dragon over the weekend has sparked interest among young people and others. Many people are asking how Apollo computers evaluated the transcendental functions like sine, arctangent, log? Thanks to NASA for sharing the source code and posting it in a public domain at GitHub.
The code is part of the source code for Luminary 1A build 099. It is part of the source code for the Command Module (CM) and here for the Lunar Lander (LM) used for Apollo Guidance Computer (AGC), for Apollo 11. The AGC is a digital computer produced for the Apollo program that was installed on board each Apollo command module (CM) and Apollo Lunar Module (LM). The AGC provided computation and electronic interfaces for guidance, navigation, and control of the spacecraft. The AGC software was written in AGC assembly language and stored on rope memory.
The AGC was designed at the MIT Instrumentation Laboratory under Charles Stark Draper, with hardware design led by Eldon C. Hall. The flight hardware was fabricated by Raytheon, whose Herb Thaler was also on the architectural team.
The codes were used to implement sine and cosine functions: see here for the command module and here for the lunar lander (it looks like it is the same code).
# Page 1102
BLOCK 02
# SINGLE PRECISION SINE AND COSINE
COUNT* $$/INTER
SPCOS AD HALF # ARGUMENTS SCALED AT PI
SPSIN TS TEMK
TCF SPT
CS TEMK
SPT DOUBLE
TS TEMK
TCF POLLEY
XCH TEMK
INDEX TEMK
AD LIMITS
COM
AD TEMK
TS TEMK
TCF POLLEY
TCF ARG90
POLLEY EXTEND
MP TEMK
TS SQ
EXTEND
MP C5/2
AD C3/2
EXTEND
MP SQ
AD C1/2
EXTEND
MP TEMK
DDOUBL
TS TEMK
TC Q
ARG90 INDEX A
CS LIMITS
TC Q # RESULT SCALED AT 1.
Below is an explanation of the code. Hats off to Nathan Tuggy at stackexchange
The comment
# SINGLE PRECISION SINE AND COSINE
indicates, that the following is indeed an implementation of the sine and cosine functions.
Information about the type of assembler used, can be found on Wikipedia.
Partial explanation of the code:
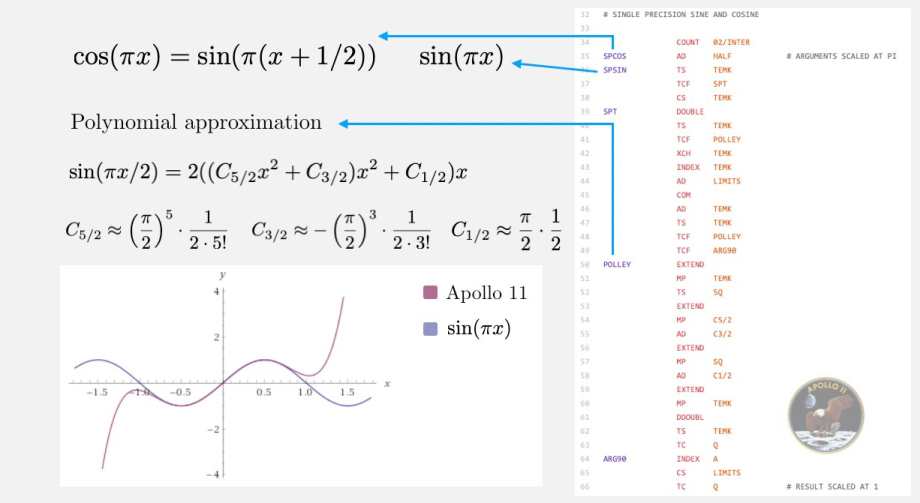
The subroutine SPSIN actually calculates sin(πx)sin(πx), and SPCOS calculates cos(πx)cos(πx).
The subroutine SPCOS first adds one half to the input, and then proceeds to calculate the sine (this is valid because of cos(πx)=sin(π(x+12))cos(πx)=sin(π(x+12))). The argument is doubled at the beginning of the SPT subroutine. That is why we now have to calculate sin(π2y)sin(π2y) for y=2xy=2x.
The subroutine POLLEY calculates an almost Taylor polynomial approximation of sin(π2x)sin(π2x). First, we store x2x2 in the register SQ (where xx denotes the input). This is used to calculate the polynomial
The values for the constants can be found in the same GitHub repository and are
which look like the first Taylor coefficients for the function 12sin(π2x)12sin(π2x).
These values are not exact! So this is a polynomial approximation, which is very close to the Taylor approximation, but even better (see below, also thanks to @uhoh and @zch).
Finally, the result is doubled with the DDOUBL command, and the subroutine POLLEY returns an approximation to sin(π2x)sin(π2x).
Note that for this polynomial approximation you only need four multiplications and two additions (MP and AD in the code). For the Apollo Guidance Computer, memory and CPU cycles were only available in small numbers.
There are some ways to increase accuracy and input range, which would have been available for them, but it would result in more code and more computation time. For example, exploiting symmetry and periodicity of sine and cosine, using the Taylor expansion for cosine, or simply adding more terms of the Taylor expansion would have improved the accuracy and would also have allowed for arbitrary large input values.
Below is an old NASA video which shows how the DSKY worked, about 6 minutes into the program: